- Visi dalykai
-
2. Kinematika
Tiesiaeigis tolyginis ir netolyginis judėjimas
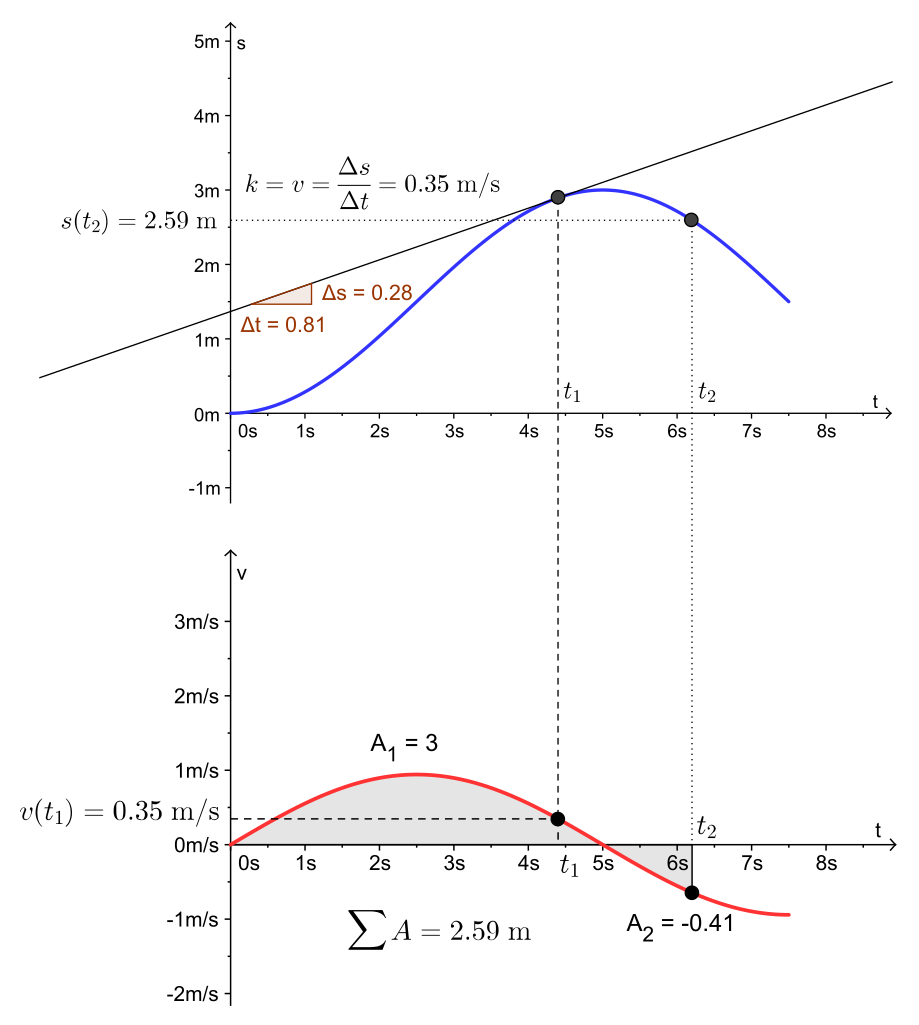
Kelias, poslinkis, greitis, pagreitis. Judėjimo lygtys x(t). Vidutinis ir momentinis greitis. Grafinė judėjimo analizė (x-t, v-t grafikai).
Skaidrių režimo valdymas
Rodykite pamoką visame ekrane.
Naudokite viršutinėje juostoje esantį pilno ekrano mygtuką, jei norite paslėpti pašalinius elementus.
Teksto dydį galite keisti mygtukais „A-“ ir „A+“, kad viskas būtų įskaitoma klasėje.
Mygtukai „Atgal“ ir „Pirmyn“ leidžia greitai pereiti tarp pamokos dalių.
Laikmatis padeda sekti pamokos tempą, o esamas laikas padeda planuoti pertraukas.
Šis turinys priklauso „Edukamentas Super“
Įsigykite „Super“ už 19,99 € / mėn. ir gaukite prieigą prie visų mokyklos dalykų.
Šioje pamokoje rasite:

Labas, kuriame turinį nuo 2019 metų!
Įsigykite „Super“ už 19,99 € / mėn. ir gaukite prieigą prie visų mokyklos dalykų.
Jūsų mokykla jau turi „Super“ sutartį? Prisijunkite naudodami savo mokyklos paskyrą.
Prieiga prie 7 dalykų (įskaitant tiksliuosius mokslus – tik „Edukamentas Super“)
Dirbtinio intelekto testai
Atsakykite savais žodžiais kaip per egzaminą! Pasitikrinkite žinias ir iškart gaukite įvertinimą su paaiškinimais, kaip gauti geresnį pažymį.
Įvairūs formatai
Mokykitės taip, kaip jums patogiausia: nuo išsamių straipsnių ir laiko juostų iki audio įrašų ir vaizdo medžiagos.
Atminties kortelės
Įsiminkite svarbiausias datas, sąvokas ir faktus greitai ir lengvai su mūsų paruoštomis kortelėmis (angliškai jos vadinasi flashcards).
Pirminiai šaltiniai
Analizuokite autentiškus istorinius dokumentus ir literatūros kūrinių ištraukas – viskas vienoje vietoje.
Tėvams: sekite progresą
Pakvieskite tėvus nemokamai stebėti mokinio progresą – arba tėvai gali nupirkti planą jums.
Mentorystė
Užduokite klausimus forume – jei atsakymo nėra mūsų medžiagoje, atsakysime mes.
Reikia „Super“ plano
Įsigykite „Super“ už 19,99 € / mėn. ir gaukite prieigą prie visų mokyklos dalykų.